FanHandler installation
FanHandler Inc. 1443 45th Ave, Salem OR 97301
For use only on P.S.C. or shaded pole motors used to drive direct-drive fans, blowers and pumps.
LOW VOLTAGE SENSORS FOR 120, 240 and 277 volt FanHandler and ZoneHandler CONTROLS
LA-120, LA-240 AND LA 277 ARE SUPPLIED WITH 1-YELLOW SENSOR.
120-15, 240-8 AND 277-8 ARE SUPPLIED WITH 1-RED SENSOR (heating) OR 1 BLUE SENSOR (cooling)
FAC-120, FAC-240 AND FAC-277 ARE SUPPLIED WITH 1-RED & 1 BLUE SENSOR
HP-120, HP-240 AND HP 277 ARE SUPPLIED WITH 1-YELLOW & 1 BLUE SENSOR
Ohm values @ 77°: Red = 30K, Blue = 5K, Yellow = 5K
ZoneHandler 120, 240 AND 277 ARE SUPPLIED WITH AN ELECTRONIC PRESSURE TRANSDUCER, STATIC PRESSURE PICK UP TUBE AND SPECIALLY DESIGNED RESTRICTORS.
FanHandler controls are ETL listed for field or factory installation under file #114704-322 as conforming to ANSI/UL-508 and CAN/CSA C22.2 NO. 14. Installation and wiring must comply with all local and national electrical codes. Only qualified HVAC technicians and service mechanics may install or adjust the FanHandler motor speed control. To do otherwise will void all warranties.
INSTALLATION
- DISCONNECT POWER TO THE EQUIPMENT
- Check operating voltage of fan, and make certain that the control is of the proper voltage and type.
- Mount the FanHandler in a location safe from weather, moisture or excessive heat. Normally this is inside the fan compartment, mounted on or near the blower.
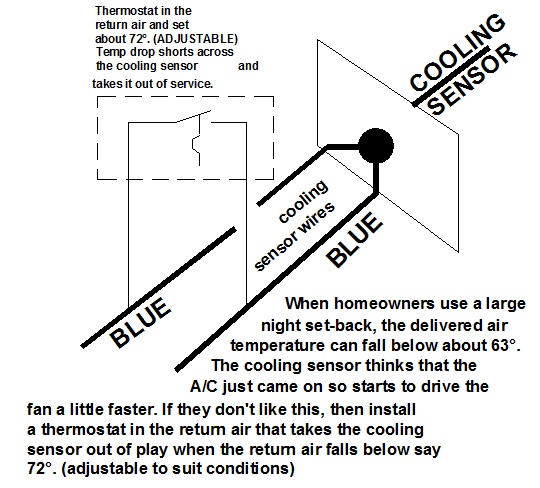
- . Locate sensors in the SUPPLY Duct were they will sense a representative sample of the air temperature being delivered to the conditioned space. This is done by drilling a 1/2” holes in the proper locations and fastening sensors to duct with two sheet metal screws each. Do not locate sensors a long distance down the duct from the heating and cooling source, and do not mount them right up close to the heat source or the a/c coil. This may result in inconsistant fan speeds. Route low voltage sensor wires (usually thermostat wire) away from high voltage wiring. Wire sensors to corresponding colored sensor wires (blue sensor to blue wires, red sensor to red wires and yellow sensor to yellow wires).
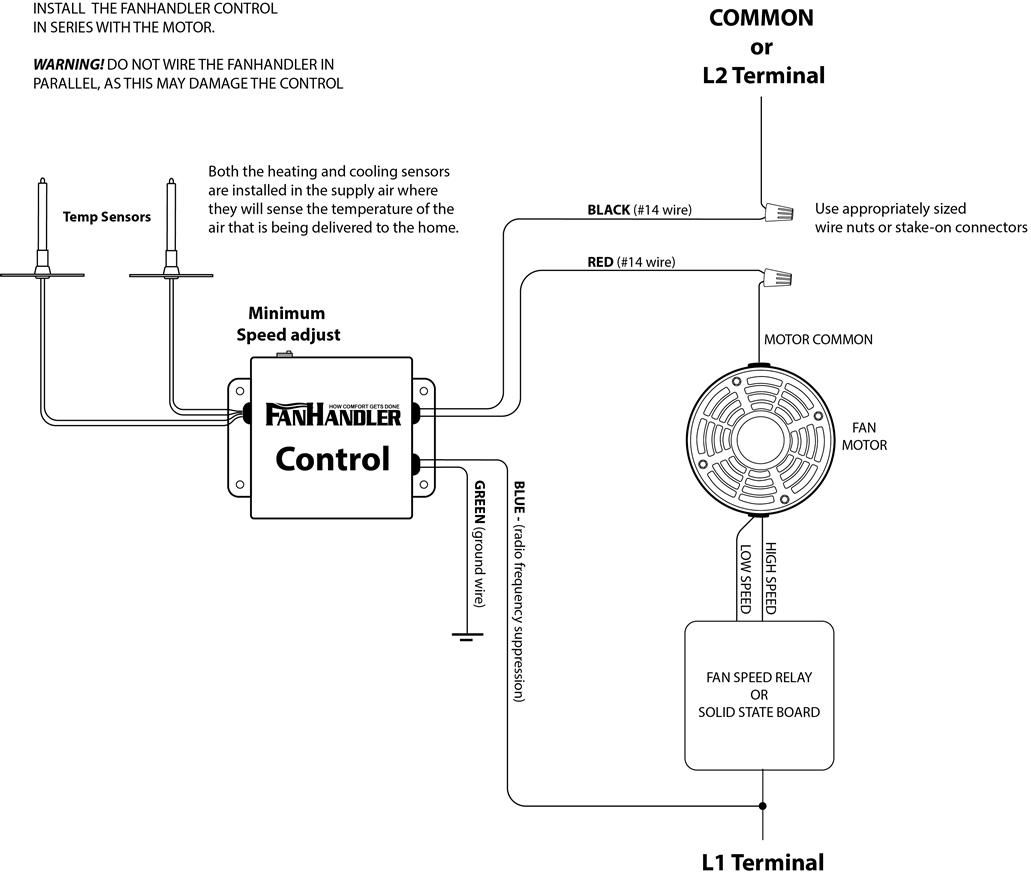
- Wire the FanHandler in series with the fan motor. The recommended placement is in the common wire from the motor.
- Double check wiring, then reapply power to the system.
- Determine mode of operation. The FanHandler and ZoneHandler controls can be operated either with the sub base to AUTO for intermittant fan operation, or to FAN ON for continuous operation.
- Set minimum speed. In many cases it is not necessary to adjust the minimum speed. However, if you want to adjust the minimum speed, it is done by turning the small screw on the blue rectangular potentiometer that is next to the fuse holder at the top of the control. This is a 25-turn pot with a clutch at both ends, so you won’t break it from over-turning. Turning the pot clockwise increases the minimum speed, and turning the pot counter clockwise lowers the minimum speed. Set the minimum speed as high as possible, without causing uncomfortable drafts. Setting the minimum speed too low (although impressive) does not properly mix the air in the home and will produce unwanted results. A rule of thumb: set minimum speed so that the furthest run will move a tissue but not cause a draft a foot from the register. The minimum speed adjustment is for setup and fine-tuning only, it should be set and left alone. If the owner wants to temporarily override or change the speed of the fan after installation, then a remote speed selector should be installed (see later in the instructions). That way your original setting is maintained while allowing the customer to override the speed as desired.
- Verify operation. Allow the system to balance out so it is delivering about 72° and is neither calling for heating nor cooling. Then set the thermostat to call for heat, as the temperature rises in the duct, the fan speed should increase. Set the thermostat to shut the heat off and observe that as the delivered air temperature drops, the fan speed will decrease to your PRE-SET minimum speed. Then set the thermostat to call for cooling, as the temperature in the duct drops the fan speed will increase and hit top speed at about 50° delivered temperature. Turn thermostat up turning off the air conditioner. Observe that while the temperature in the duct approaches room temperature, the FanHandler control will smoothly decrease the fan speed back to your minimum speed setting.
ALL FanHandler and ZoneHandler
Controls have the same configuration for minimum speed setting.

Only the #14 black wire (line in) and the #14 red wire (line out to motor) operate the motor. The blue wire is used to eliminate radio frequency noise, and the green wire is for ground. These controls can be installed in the hot (L1) or the common line (or L2). FanHandler controls can be used on any speed tap or switched between speed taps. They can be switched on and off or run continuously. The low voltage #18 wires located next to the ETL label are connected to the sensors and can be extended by using low voltage thermostat wire.
!
Branch Line Protection
All 120 volt models are rated at 15 amps, 60 Hz maximum. All 240 and 277 volt models are rated at 8 amps, 60 Hz maximum. It is the installer’s responsibility to provide branch line circuit protection to the FanHandler circuit of no more than 15 amps. (usually the equipment fusing will qualify for this requirement).
NOTE: ALL FANHANDLER CONTROLS ARE DESIGNED FOR USE AS OPERATING CONTROLS ONLY. THEY ARE NOT LIMIT OR SAFETY CONTROLS. IT IS THE INSTALLER’S RESPONSIBILITY TO TEST OR INSTALL SAFETY AND/OR LIMIT CONTROLS WHERE AN OPERATING CONTROL FAILURE WOULD RESULT IN PERSONAL INJURY AND/OR DAMAGE TO PROPERTY.
GROUNDING
For electrical safety and correct operation, be sure to properly ground the entire furnace and air conditioner system, including associated devices and the FanHandler. Devices such as electronic air cleaners, spark ignitors, etc. if not properly grounded will cause “motor bumping”. Improper grounding of the FanHandler control and motor may result in AM band radio noise.
INSTALLING IN THE COMMON WIRE (Preferred method)
TROUBLE SHOOTING GUIDE
· MOTOR STAYS AT HIGH SPEED - Minimum speed adjustment set too high. Control bypassed by relay or switch. Wires leading to the cooling sensor (this is the most common reason) are open. Heating sensor wire or sensor shorted. Sensors mixed.
· MOTOR STAYS AT LOW SPEED - On heating, the heating sensor or wire open. On cooling, the cooling sensor or wire shorted. Red heating sensor measures about 30K ohms @ 78°. Blue cooling sensor and yellow heating sensors measure about 5k ohms at 78°. These sensors are much more accurate than the average service ohmeter.
· MOTOR GROWLING OR BUMPING - Incompatible motor, poor grounding of equipment. Sensors shorted to ground.
(IMPORTANT) ------ MOTOR SELECTION ------ (IMPORTANT)
If you or your customer is unwilling to replace an incompatable motor, we recommend that you not purchase or install FanHandler controls. Equipment manufacturers have been using higher quality motors lately. We suspect that this is because of extended warrantees. If you install a number of FanHandler controls, you will encounter poor quality direct drive fan motors. These motors may be built to meet a price criteria rather than a quality specification. These motors do not contain adequate copper windings or iron laminates to allow the motor to follow the fan laws when reducing speed. These motors are usually constructed with loose stator to rotor spacing tolerances. Or a motor on the job might have been banging on and off for years and not serviced, so the bearings are worn. If a motor heats-up and/or growls at low speed, it should be replaced with a high quality motor designed for general use.
Quality is the only factor in determining a motor’s fitness for speed regulation. Determine motor fitness on a case by case basis. It is impractical for us to keep up with changes that equipment manufacturers make in the motors that they install. Baldor (the big dog of industrial motors) is building high quality, commercial/industrial quality, motors to our specifications. We offer these motors to FanHandler contractors only at very affordable prices. I.e. We aren’t making money on them. You will not know what a super high-quality motor is, until you have experience with a Baldor motor!
· RADIO NOISE - Improperly grounded motor or HVAC system.
· MOTOR STAYS OFF - Power off to motor (circuit breaker, fuse, or fan compartment switch, open).
LA-120 & LA-240 INSTRUCTIONS
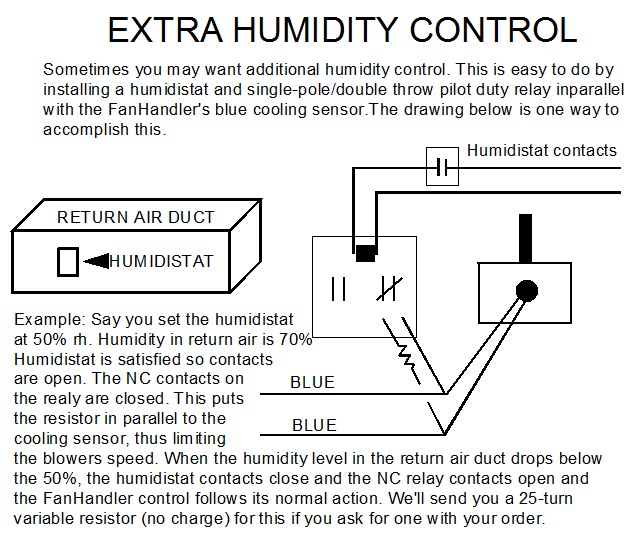
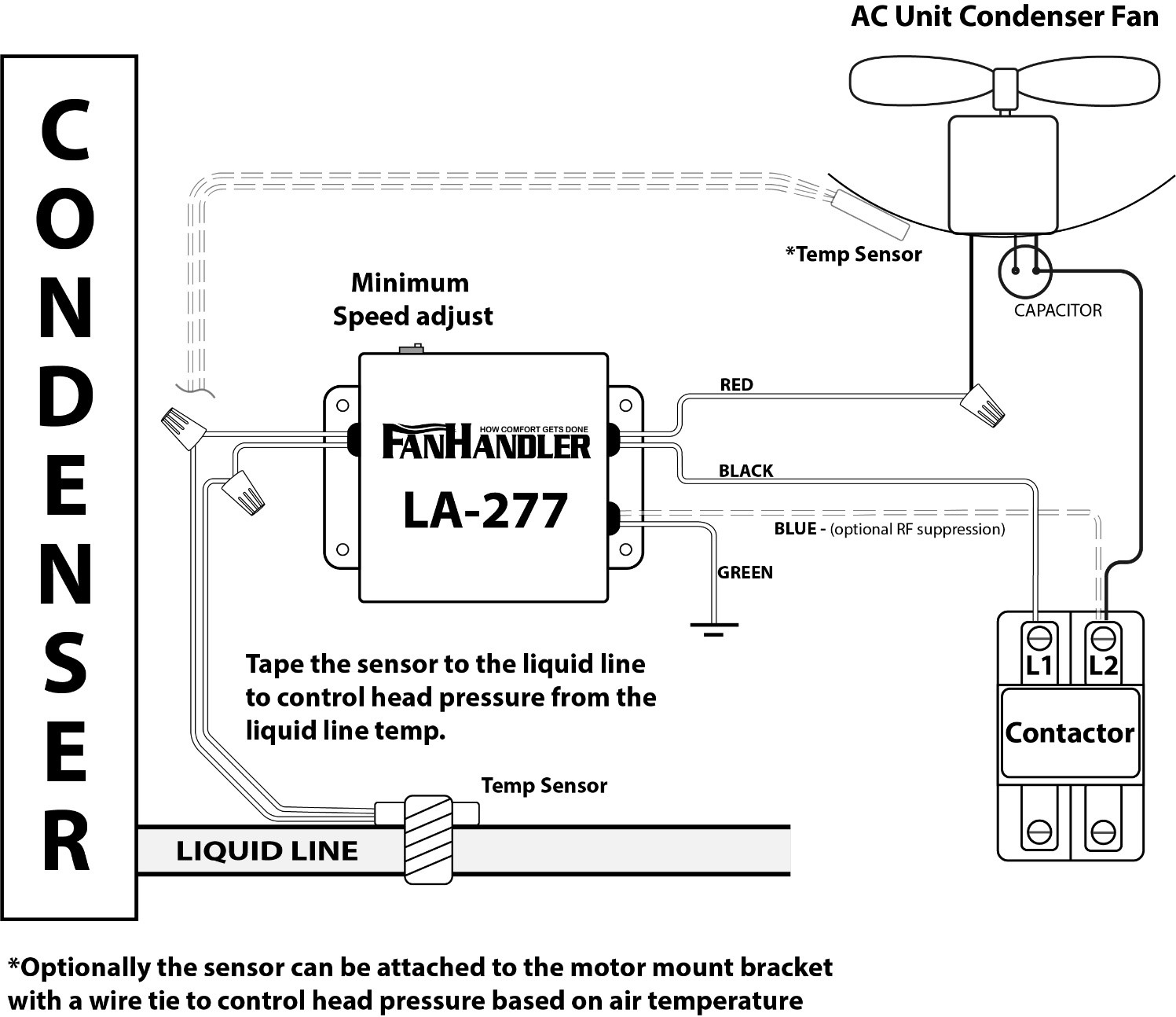
FanHandler LA models are used to control refrigerant head pressure. They are basically wired the same as the other models. The only difference is that the sensor is located in the air stream leaving the condenser coil or attached to the liquid line (recommended best) just as it leaves the condenser. Use insulated black tape which works very well. Protect the control box from the weather by installing it in the control compartment or using a weather-tight box. Set the minimum speed so that the condenser fan is able to turn when power is applied to motor. LA controls are aoften used to control the speed of the circulating pump for head pressure control in water source heat pump applications. This is also a very useful tool to use when setting refrigerant charge in cold weather. It beats “tenting” by a long shot.
CONTROLLING HEAD PRESSURE


MADE TO OUR SPECIFICATIONS, FOR OUR SUPER HIGH QUALITY MOTOR SPEED CONTROLS.
We’ve tested these, and have NEVER seen a better motor.
Whisper Quiet, responsive, super energy efficient & Country-boy strong
We’ve even run one for three weeks at about 100 rpm. It is cool and super quiet even at that speed!!!!
Industrial/commercial quality, ball bearings, electrically reversible, 48 frame, 1075 rpm, 3-speed, 50° rise,super quiet, super high efficiency. Just like FanHandler, Baldor does not cut corners.

Blower motor quality varies greatly. Indicators of unacceptable motor quality are: loud growl at low speed, overheating and amp draw that doesn’t drop as motor speed decreases. A motor may have been banging on and off for several years and, because of bearing wear, the rotor is no longer aligned with the stator and other motors were just built that way. All motor manufacturers know how to build high quality/high impedance motors. We are confident that market forces govern their quality decisions.
Equipment manufacturers are not obligated to install motors to meet our standards. Some manufacturers are installing very high quality motors and some are short on copper windings and iron laminates. We stopped trying to keep up with who’s installing what motor.
Several years ago, we got fed-up with being blamed for poor motor performance associated with speed control.
Our response to this is to make available the best quality motor we can find. Doing so, keeps us, and our customers, at the forefront of comfort, efficiency and quality.
We asked Baldor Electric (the big dog of commercial/industrial motors) to build a motor for the FanHandler and then tell us what it cost. We sent them several of our controls and they came up with the best motor we’ve seen. The cost was surprisingly low.
These motors are available to FanHandler customers only. These motors are not a profit item for us. (We make our money from FanHandler and ZoneHandler control sales.) We are pleased to make these motors available to our customers who use one with each control for the best possible results from their installations or have run into a motor that doesn’t perform to expectations.
These motors are only available to FanHandler customers.
FanHandler Inc - Salem, OR
ALL FanHandler and ZoneHandler
Controls have the same configuration for minimum speed setting.
